- Tue 10 April 2018
- Machine Learning
- William Miller
- #machine learning, #data analysis, #data visualization, #Kaggle.com, #Titanic, #XGBoost, #Random Forest
Import libraries
import pandas as pd
import numpy as np
import random as rnd
import seaborn as sns
import matplotlib.pyplot as plt
Load data and perform initial evaluation
At the outset, I will print out an information call for the training and testing sets and sample of the training set. This will be a lot to look through, up front, but it will be valuable for planning how to proceed.
train_df = pd.read_csv('./input/train.csv')
test_df = pd.read_csv('./input/test.csv')
combine = [train_df, test_df]
for data in combine:
print(data.info())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 714 non-null float64
SibSp 891 non-null int64
Parch 891 non-null int64
Ticket 891 non-null object
Fare 891 non-null float64
Cabin 204 non-null object
Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB
None
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 418 entries, 0 to 417
Data columns (total 11 columns):
PassengerId 418 non-null int64
Pclass 418 non-null int64
Name 418 non-null object
Sex 418 non-null object
Age 332 non-null float64
SibSp 418 non-null int64
Parch 418 non-null int64
Ticket 418 non-null object
Fare 417 non-null float64
Cabin 91 non-null object
Embarked 418 non-null object
dtypes: float64(2), int64(4), object(5)
memory usage: 36.0+ KB
None
print(train_df.sample(20))
PassengerId Survived Pclass \
440 441 1 2
518 519 1 2
362 363 0 3
584 585 0 3
835 836 1 1
77 78 0 3
866 867 1 2
496 497 1 1
201 202 0 3
246 247 0 3
780 781 1 3
239 240 0 2
99 100 0 2
365 366 0 3
550 551 1 1
814 815 0 3
340 341 1 2
212 213 0 3
783 784 0 3
671 672 0 1
Name Sex Age SibSp \
440 Hart, Mrs. Benjamin (Esther Ada Bloomfield) female 45.0 1
518 Angle, Mrs. William A (Florence "Mary" Agnes H... female 36.0 1
362 Barbara, Mrs. (Catherine David) female 45.0 0
584 Paulner, Mr. Uscher male NaN 0
835 Compton, Miss. Sara Rebecca female 39.0 1
77 Moutal, Mr. Rahamin Haim male NaN 0
866 Duran y More, Miss. Asuncion female 27.0 1
496 Eustis, Miss. Elizabeth Mussey female 54.0 1
201 Sage, Mr. Frederick male NaN 8
246 Lindahl, Miss. Agda Thorilda Viktoria female 25.0 0
780 Ayoub, Miss. Banoura female 13.0 0
239 Hunt, Mr. George Henry male 33.0 0
99 Kantor, Mr. Sinai male 34.0 1
365 Adahl, Mr. Mauritz Nils Martin male 30.0 0
550 Thayer, Mr. John Borland Jr male 17.0 0
814 Tomlin, Mr. Ernest Portage male 30.5 0
340 Navratil, Master. Edmond Roger male 2.0 1
212 Perkin, Mr. John Henry male 22.0 0
783 Johnston, Mr. Andrew G male NaN 1
671 Davidson, Mr. Thornton male 31.0 1
Parch Ticket Fare Cabin Embarked
440 1 F.C.C. 13529 26.2500 NaN S
518 0 226875 26.0000 NaN S
362 1 2691 14.4542 NaN C
584 0 3411 8.7125 NaN C
835 1 PC 17756 83.1583 E49 C
77 0 374746 8.0500 NaN S
866 0 SC/PARIS 2149 13.8583 NaN C
496 0 36947 78.2667 D20 C
201 2 CA. 2343 69.5500 NaN S
246 0 347071 7.7750 NaN S
780 0 2687 7.2292 NaN C
239 0 SCO/W 1585 12.2750 NaN S
99 0 244367 26.0000 NaN S
365 0 C 7076 7.2500 NaN S
550 2 17421 110.8833 C70 C
814 0 364499 8.0500 NaN S
340 1 230080 26.0000 F2 S
212 0 A/5 21174 7.2500 NaN S
783 2 W./C. 6607 23.4500 NaN S
671 0 F.C. 12750 52.0000 B71 S
The description of the data reveals a few problems:
- Age entries are incomplete in both training and testing data sets. These will need to be filled in either with mean ages, or with ages predicted by other data that correlates.
- "Cabin" data is recorded very infrequently.
- "Ticket" data appears noisy and difficult to parse, if it turns out to be useful at all.
- A couple of entries in "Embarked" are missing.
- One entry in "Fare" is missing in the test data.
The sample reveals that there are also some adjustments that need to be made to the data:
- "Sex" should be simplified to "0" and "1"
- "Embarked" should be mapped to numerical values
- Since all names include titles, it may be possible to isolate the titles and make use of them
- "Ticket" can likely be dropped
- Fill in trivial missing values and convert to string categories to numerical
- Fill missing values in "Embarked"
- Fill missing values in "Fare"
- Change "Sex" and "Embarked" to numerical values.
- Add additional features, where possible.
- Create "Family_Size" feature from "SibSp" and "Parch"
- If possible, extract titles from "Names" and replace names with titles.
- Determine best method for filling in missing age data.
- Fill in missing age data
- Make a test run of XGBoost and Random Forest classifiers to see which makes the most accurate predictions.
- Use the results of this test run to eliminate the least useful features in the dataset, if necessary.
- If the performance of the classifiers is similar:
- Refine the tuning of each classifier
- Compare the predictions of the re-tuned classifiers
- Select the classifier that consistently makes the most accurate predictions from test data
- Deploy the best algorithm and evalute the results (in this case, run it against the full set of test data and submit the results to the Kaggle competition).
- Mean test scores at a gamma value of 0 is highly inconsistent, while they are much more consistent at a value of 5. Retaining a value of 1 would likely result in a lot of variation in accuracy when applying this classifier to new data.
- The minimum child weight clearly peaks at 4, though values of 2 and 3 are worth considering due to their higher degree of consistency. At a value of 1 the algorithm is not conservative enough and likely overfits the training data. At a value of 5 it is overly conservative and loses a significant amount of accuracy.
- Going from a learning weight of 0.1 to 0.2, there is some increase in mean test score values, though the top of its range in slightly lower. It might be worth exploring values that are slightly higher.
- While the highest test scores for maximum depth of 12 are higher than those for values of 7 and 9, the difference is not very significant, and there is slightly more variation within scores for this value. Since increases in maximum depth contributes to overfitting, the increased variation in test values observed at a value of 12 indicates that increasing the value further will likely result in overfitting. It appears that a value of 5 yields greater consistency with a mean test score that is roughly the same.
- Mean test scores appear to increase with the number of estimators, but accuracy seems to level off above a number of 100. This indicates that increases in amount of computation time may not be very useful above this level.
- The minimum samples per leaf clearly peaks at 8. A value of 4 yields similar mean test scores, but with a much lower precision. For more consistent results when presented with new data, a value of 8 here would be best.
- When the maximum number of features is 80% of those in the data set, the highest test scores return tend to be higher, but with a large cost to precision. The mean result with trees utilizing 40% of the features is higher, and the mean test score results are more consistent.
- As with gradient boosting, increasing the maximum depth decreases precision dramatically. Exploring values below 15 might be beneficial.
- Mean test scores appear to increase with the number of estimators. Exploring numbers above 1000 might be beneficial, but any increase in accuracy above this would result in a significant investment of processing time.
Wrangle Data
Make changes determined in initial evaluation, in the following order:
From there, I will use XGBoost and RandomForest classifiers to make predictions from the resulting data, tune them to consistently yield accurate predictions, then choose the best of the two.
Before proceeding any further, I will go ahead and set the index to "PassengerId"
train_df = train_df.set_index('PassengerId')
test_df = test_df.set_index('PassengerId')
combine = [train_df, test_df]
Fill trivial missing values, convert categorical strings to numerical
Fill missing values in "Embarked" and "Fare"
port_mode = train_df.Embarked.dropna().mode()[0]
fare_med = test_df.Fare.dropna().median()
for data in combine:
data['Embarked'] = data['Embarked'].fillna(port_mode)
data['Fare'] = data ['Fare'].fillna(fare_med)
print(port_mode)
print(fare_med)
S
14.4542
Map "Sex" and "Embarked" to numerical values
sex_mapping = {"female": 0, "male": 1}
embarked_mapping = {'S': 0, 'C': 1, 'Q': 2}
for data in combine:
data['Sex']=data['Sex'].fillna(0)
data['Embarked']=data['Embarked'].fillna(0)
data['Sex']=data['Sex'].map(sex_mapping).astype(int)
data['Embarked']=data['Embarked'].map(embarked_mapping).astype(int)
print(train_df.sample(10))
Survived Pclass \
PassengerId
729 0 2
732 0 3
325 0 3
716 0 3
329 1 3
625 0 3
257 1 1
395 1 3
85 1 2
828 1 2
Name Sex Age \
PassengerId
729 Bryhl, Mr. Kurt Arnold Gottfrid 1 25.0
732 Hassan, Mr. Houssein G N 1 11.0
325 Sage, Mr. George John Jr 1 NaN
716 Soholt, Mr. Peter Andreas Lauritz Andersen 1 19.0
329 Goldsmith, Mrs. Frank John (Emily Alice Brown) 0 31.0
625 Bowen, Mr. David John "Dai" 1 21.0
257 Thorne, Mrs. Gertrude Maybelle 0 NaN
395 Sandstrom, Mrs. Hjalmar (Agnes Charlotta Bengt... 0 24.0
85 Ilett, Miss. Bertha 0 17.0
828 Mallet, Master. Andre 1 1.0
SibSp Parch Ticket Fare Cabin Embarked
PassengerId
729 1 0 236853 26.0000 NaN 0
732 0 0 2699 18.7875 NaN 1
325 8 2 CA. 2343 69.5500 NaN 0
716 0 0 348124 7.6500 F G73 0
329 1 1 363291 20.5250 NaN 0
625 0 0 54636 16.1000 NaN 0
257 0 0 PC 17585 79.2000 NaN 1
395 0 2 PP 9549 16.7000 G6 0
85 0 0 SO/C 14885 10.5000 NaN 0
828 0 2 S.C./PARIS 2079 37.0042 NaN 1
Extract additional features
It is always worth considering if additional features can be created out of existing ones that might prove useful for the purposes of prediction. It is always possible to see after a prediction is made which features were most useful, and anything that proved to be useless (or mostly so) can be dropped.
Investigate NaN significance
Before filling NaN data, it is worth exploring if there is a significant difference in survival rate between the data that is NaN versus that which is not. If there is a difference, it may be worth creating new binary features that store whether or not a value was NaN for that entry.
print('Mean survival rate: {0:.3f}'.format(train_df['Survived'].mean()), '\n')
print('Cabin not Nan mean survival rate: {0:.3f}'.format(train_df[train_df['Cabin'].notnull()]['Survived'].mean()))
print('Cabin NaN mean survival rate: {0:.3f}'.format(train_df[train_df['Cabin'].isnull()]['Survived'].mean()), '\n')
print('Age not Nan mean survival rate: {0:.3f}'.format(train_df[train_df['Age'].notnull()]['Survived'].mean()))
print('Age NaN mean survival rate: {0:.3f}'.format(train_df[train_df['Age'].isnull()]['Survived'].mean()))
Mean survival rate: 0.384
Cabin not Nan mean survival rate: 0.667
Cabin NaN mean survival rate: 0.300
Age not Nan mean survival rate: 0.406
Age NaN mean survival rate: 0.294
It appears that it will definitely be worth accounting for whether or not this data was present. For reasons that are not apparent from the data, there was 36.7% greater chance that a passenger survived if we have data for the cabin they stayed in. Though it's not quite as pronounced, there is also a significant difference in survival chance between passengers who were missing age data and those who were not.
Create "Cabin_Record" and "Age_Record" features
train_df['Cabin_Record'] = train_df['Cabin'].where(train_df['Cabin'].isnull(), 1).fillna(0).astype('int64')
test_df['Cabin_Record'] = test_df['Cabin'].where(test_df['Cabin'].isnull(), 1).fillna(0).astype('int64')
train_df['Age_Record'] = train_df['Age'].where(train_df['Age'].isnull(), 1).fillna(0).astype('int64')
test_df['Age_Record'] = test_df['Age'].where(test_df['Age'].isnull(), 1).fillna(0).astype('int64')
train_df[['Cabin', 'Cabin_Record', 'Age', 'Age_Record']].sample(10)
| Cabin | Cabin_Record | Age | Age_Record | |
|---|---|---|---|---|
| PassengerId | ||||
| 696 | NaN | 0 | 52.0 | 1 |
| 666 | NaN | 0 | 32.0 | 1 |
| 262 | NaN | 0 | 3.0 | 1 |
| 761 | NaN | 0 | NaN | 0 |
| 24 | A6 | 1 | 28.0 | 1 |
| 404 | NaN | 0 | 28.0 | 1 |
| 448 | NaN | 0 | 34.0 | 1 |
| 385 | NaN | 0 | NaN | 0 |
| 333 | C91 | 1 | 38.0 | 1 |
| 784 | NaN | 0 | NaN | 0 |
Create "Family_Size" feature
One first possible additional feature to consider comes from the fact that Sibsp and Parch have some ambiguity built into them. It seems likely that there would be a significant difference in survival rate between people who traveled with their spouses versus their siblings, or parents versus their children. It might be beneficial to roll these into a single statistic of family size, as this will eliminate the inconsistency that is present in the 'SibSp' and 'Parch' data.
train_df['Family_Size'] = train_df['SibSp'] + train_df['Parch']
test_df['Family_Size'] = test_df['SibSp'] + test_df['Parch']
train_df[train_df.columns].corr()['Parch']
Survived 0.081629
Pclass 0.018443
Sex -0.245489
Age -0.189119
SibSp 0.414838
Parch 1.000000
Fare 0.216225
Embarked -0.078665
Cabin_Record 0.036987
Age_Record 0.124104
Family_Size 0.783111
Name: Parch, dtype: float64
Create "Title" feature
One can see from a sample of the data above that each name has an associated title, and that each appears to follow a similar format. While I've not shown this due to the amount of space required, I took several large samples to verify that this is the case for at least enough of the data that it might be useful. After extracting the "Title" info, I will look at how many titles their are, see if any entries are lacking titles, or if any titles may not be useful. It is simple enough to use regular expressions to extract the titles from the names.
for data in combine:
data['Title'] = data.Name.str.extract(' ([A-za-z]+)\.', expand=False)
print(train_df.groupby('Title').agg({'Title':'count', 'Age':'mean', 'Survived': 'mean'}).reindex())
print(test_df.groupby('Title').count().reindex())
Title Age Survived
Title
Capt 1 70.000000 0.000000
Col 2 58.000000 0.500000
Countess 1 33.000000 1.000000
Don 1 40.000000 0.000000
Dr 7 42.000000 0.428571
Jonkheer 1 38.000000 0.000000
Lady 1 48.000000 1.000000
Major 2 48.500000 0.500000
Master 40 4.574167 0.575000
Miss 182 21.773973 0.697802
Mlle 2 24.000000 1.000000
Mme 1 24.000000 1.000000
Mr 517 32.368090 0.156673
Mrs 125 35.898148 0.792000
Ms 1 28.000000 1.000000
Rev 6 43.166667 0.000000
Sir 1 49.000000 1.000000
Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked \
Title
Col 2 2 2 2 2 2 2 2 2 2
Dona 1 1 1 1 1 1 1 1 1 1
Dr 1 1 1 1 1 1 1 1 1 1
Master 21 21 21 17 21 21 21 21 2 21
Miss 78 78 78 64 78 78 78 78 11 78
Mr 240 240 240 183 240 240 240 240 42 240
Mrs 72 72 72 62 72 72 72 72 32 72
Ms 1 1 1 0 1 1 1 1 0 1
Rev 2 2 2 2 2 2 2 2 0 2
Cabin_Record Age_Record Family_Size
Title
Col 2 2 2
Dona 1 1 1
Dr 1 1 1
Master 21 21 21
Miss 78 78 78
Mr 240 240 240
Mrs 72 72 72
Ms 1 1 1
Rev 2 2 2
It appears that title extraction worked and that the data may prove useful. Fortunately, every passenger has an associated title and there appear to be significant differences between the titles when it comes to average survival rate, sex, and age. There are, however, a large number of titles that represent an insignificant portion of the population, and these are not useful for the purposes of prediction, which means this requires some additional processing.
Tidy up title data, convert to numerical values
I will combine synonymous titles (e.g. "Ms" and "Miss"). I will remove the titles that occur with a frequency that is unlikely to be useful. I notice that the majority of infrequent titles correlate with the careers of males over 40, so I will combine these into their own category.
for data in combine:
data['Title']=data['Title'].replace(['Capt', 'Col', 'Don', 'Dr', 'Major', 'Rev', 'Sir'], 'CareerMale')
data['Title']=data['Title'].replace('Jonkheer', 'Mr')
data['Title']=data['Title'].replace(['Countess', 'Mme', 'Lady'], 'Mrs')
data['Title']=data['Title'].replace(['Mlle', 'Ms'], 'Miss')
print(train_df.groupby('Title').agg({'Title':'count', 'Age':'mean', 'Survived': 'mean'}).reindex(), '\n')
fig, ax = plt.subplots(figsize=([12,8]))
ax = sns.violinplot(x=train_df['Title'], y=train_df['Age'])
ax = sns.swarmplot(x=train_df['Title'], y=train_df['Age'], size = 4, color = 'black', alpha = 0.5)
plt.show()
Title Age Survived
Title
CareerMale 20 46.473684 0.300000
Master 40 4.574167 0.575000
Miss 185 21.845638 0.702703
Mr 518 32.382206 0.156371
Mrs 128 35.873874 0.796875
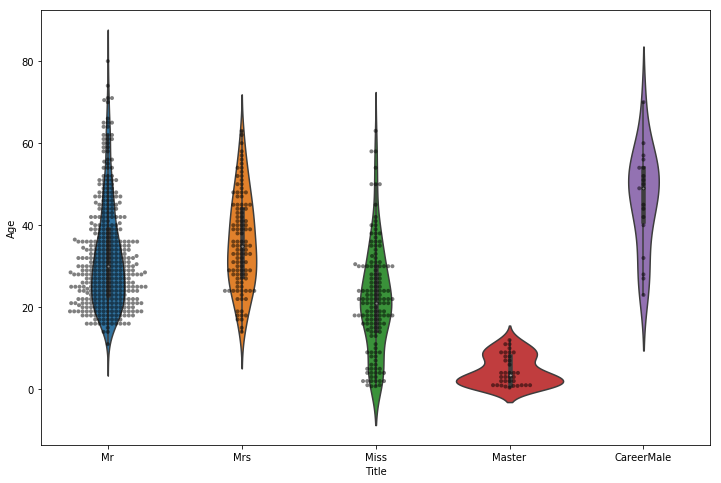
It seems highly likely that there would be some kind of relationship between the "Title" and "Family_Size" features I've created. I will plot the two of those together and see if anything stands out.
fig = (train_df.groupby(['Title', 'Survived', 'Family_Size'])
.mean()
.reset_index()
.pipe((sns.factorplot, 'data'), x='Title', y='Family_Size', hue='Survived'))
plt.show()
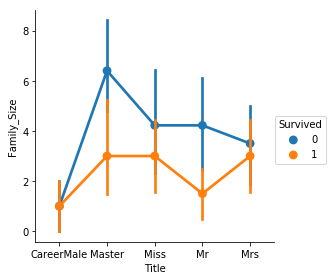
The relationships here are obvious - those in the "CareerMale" category tended to travel with one other person, those in "Master" were in a group with at least 2 others (parents), and so on. It also seems clear that the higher a passenger's family size, the lower their chance of survival.
Now to convert the title strings to numerical for future conversion to categories.
title_mapping = {'CareerMale': 1, 'Mrs': 2, 'Mr': 3, 'Miss': 4, 'Master': 5}
for data in combine:
data['Title'] = data['Title'].map(title_mapping)
data['Title'] = data['Title'].fillna(0)
data['Title'] = data['Title'].astype(int)
train_df = train_df.drop('Name', axis=1)
test_df = test_df.drop('Name', axis=1)
combine = [train_df, test_df]
Explore age significance.
I want to explore the hypothesis that accurately filling in the missing age data (as opposed to simply filling missing ages with the mean age) may have an effect in the accuracy of survival prediction. This requires that I first look at whether certain ages actually correlate to survival rates or not.
fig, ax = plt.subplots(figsize=([10,6]))
ax.hist(x=[train_df[train_df['Survived'] == 0]['Age'].dropna(),
train_df[train_df['Survived'] == 1]['Age'].dropna()],
bins = 20, edgecolor = 'black', stacked=True, alpha = 0.75,
label = ['Not Survived', 'Survived'])
ax.legend()
plt.show()
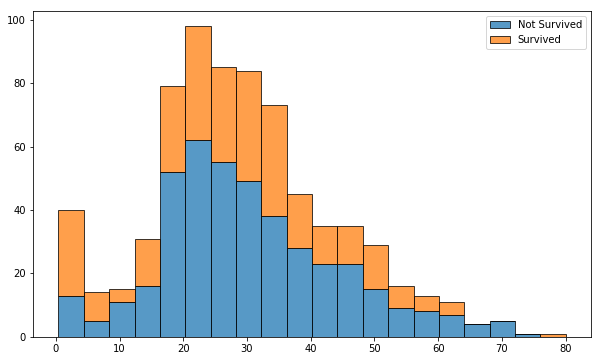
It is clear that passengers under 18 had a higher survival rate. Passengers between the ages of 20 and 30 had a much lower survival rate than any other age. It is also apparent that a very low number of people over the age of 60 survived.
Complete missing age data
First I will see which features in the dataset have the highest correlation with "Age".
print(train_df[train_df.columns].corr()['Age'])
Survived -0.077221
Pclass -0.369226
Sex 0.093254
Age 1.000000
SibSp -0.308247
Parch -0.189119
Fare 0.096067
Embarked 0.010171
Cabin_Record 0.249732
Age_Record NaN
Family_Size -0.301914
Title -0.510098
Name: Age, dtype: float64
It is clear that "Title" has the highest corrleation, followed by "Pclass" and "Family_Size".
print(train_df.groupby('Title').agg({'Title': 'count', 'Age':'mean', 'Survived':'mean'}), '\n')
print(train_df.groupby('Pclass').agg({'Pclass': 'count', 'Age':'mean', 'Survived':'mean'}), '\n')
print(train_df.groupby('Family_Size').agg({'Title': 'count', 'Age':'mean', 'Survived':'mean'}), '\n')
Title Age Survived
Title
1 20 46.473684 0.300000
2 128 35.873874 0.796875
3 518 32.382206 0.156371
4 185 21.845638 0.702703
5 40 4.574167 0.575000
Pclass Age Survived
Pclass
1 216 38.233441 0.629630
2 184 29.877630 0.472826
3 491 25.140620 0.242363
Title Age Survived
Family_Size
0 537 32.220297 0.303538
1 161 31.391511 0.552795
2 102 26.035806 0.578431
3 29 18.274815 0.724138
4 15 20.818182 0.200000
5 22 18.409091 0.136364
6 12 15.166667 0.333333
7 6 15.666667 0.000000
10 7 NaN 0.000000
"Title" shows by far the highest correlation with "Age". "Pclass" does show a decent amount of difference in age between each class of passengers, with first class passengers tending to be older. "Parch" and "SibSp" each have a significant downside in that the majority of the data in each fall into a single category. While this is slightly less pronounced in "Family_Size", the first two categories have very little difference in average age and comprise the vast majority of that data.
I will opt for a strategy of computing missing age data from averages using "Title" and "Pclass", which have the highest correlation with age by a large margin and have the added benefit of not creating large numbers of sub-groups when taking averages from grouped data.
print(train_df.groupby(['Pclass', 'Title']).agg({'Age':['mean','count'],
'Survived': 'mean'}), '\n')
Age Survived
mean count mean
Pclass Title
1 1 49.727273 11 0.500000
2 40.405405 37 0.977778
3 41.539773 88 0.342593
4 29.744681 47 0.958333
5 5.306667 3 1.000000
2 1 42.000000 8 0.000000
2 33.682927 41 0.902439
3 32.768293 82 0.087912
4 22.560606 33 0.942857
5 2.258889 9 1.000000
3 2 33.515152 33 0.500000
3 28.724891 229 0.112853
4 16.123188 69 0.500000
5 5.350833 24 0.392857
It is readily apparent that there is significant variation in age between each group. While it appears that some groups are still relatively large, there appears to be a larger deviation in the ages and survival rates between them. This seems to indicate that filling in the missing ages using these groups might improve our prediction.
Impute mean ages
One potential pitfall to keep in mind while doing this is that the smaller the subgroups get, the higher the likelihood they might be composed entirely of NaN values and would cause some age data to remain missing. In case I want to experiment with adding any additional sub-groups to aid in imputing missing "Age" data in the future, I'll write the code to impute the missing ages for the smallest subgroups, then moves up the hierarchy of groups until it's imputing from the most inclusive.
index_list = ['Pclass', 'Title']
index_length = len(index_list)
for end_index in range(0, index_length - 1):
train_df['Age'] = train_df.groupby(index_list[0:index_length - end_index])['Age']\
.apply(lambda x: x.fillna(x.mean())).astype('float32')
test_df['Age'] = test_df.groupby(index_list[0:index_length - end_index])['Age']\
.apply(lambda x: x.fillna(x.mean())).astype('float32')
drop_list = ['Cabin', 'Ticket']
train_df = train_df.drop(drop_list, axis=1)
test_df = test_df.drop(drop_list, axis=1)
train_df.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 891 entries, 1 to 891
Data columns (total 12 columns):
Survived 891 non-null int64
Pclass 891 non-null int64
Sex 891 non-null int64
Age 891 non-null float32
SibSp 891 non-null int64
Parch 891 non-null int64
Fare 891 non-null float64
Embarked 891 non-null int64
Cabin_Record 891 non-null int64
Age_Record 891 non-null int64
Family_Size 891 non-null int64
Title 891 non-null int64
dtypes: float32(1), float64(1), int64(10)
memory usage: 127.0 KB
Test Algorithms for Best Prediction
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
def display_scores(algorithm, scores):
print(algorithm, ' Scores:', scores * 100)
print('Mean:', scores.mean() * 100)
print('Standard Deviation', scores.std() * 100, '\n')
X_train = train_df.copy().drop('Survived', axis=1)
y_train = train_df['Survived']
x_test = test_df.copy()
xgb_try = XGBClassifier()
rfc_try = RandomForestClassifier()
clf_list = [xgb_try, rfc_try]
clf_name_list = ['Gradient Boosting', 'Random Forest']
clf_score_dict = dict.fromkeys(clf_name_list, 0)
clf_features_dict = dict.fromkeys(clf_name_list, 0)
for clf in clf_list:
clf_name = clf_name_list[clf_list.index(clf)]
clf.fit(X_train, y_train)
clf_scores = cross_val_score(clf, X_train, y_train, scoring='accuracy', cv=10)
clf_score_dict[clf_name] = list(clf_scores)
display_scores(clf, clf_scores)
if clf_name in clf_name_list:
clf_features_dict[clf_name] = list(clf.feature_importances_)
XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bytree=1, gamma=0, learning_rate=0.1, max_delta_step=0,
max_depth=3, min_child_weight=1, missing=None, n_estimators=100,
n_jobs=1, nthread=None, objective='binary:logistic', random_state=0,
reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
silent=True, subsample=1) Scores: [ 81.11111111 81.11111111 77.52808989 88.76404494 91.01123596
83.14606742 83.14606742 78.65168539 84.26966292 85.22727273]
Mean: 83.3966348882
Standard Deviation 3.98034954593
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=1,
oob_score=False, random_state=None, verbose=0,
warm_start=False) Scores: [ 76.66666667 77.77777778 76.40449438 86.51685393 83.14606742
85.39325843 82.02247191 75.28089888 83.14606742 89.77272727]
Mean: 81.6127284077
Standard Deviation 4.64958839675
While the above is a thorough textual representation of how each classifier performs, it can be a lot to parse, so I'm going to translate this to a visual format.
clf_score_df = pd.DataFrame.from_dict(clf_score_dict, orient='columns')
ax = sns.boxplot(data=clf_score_df, orient='h')
ax = sns.swarmplot(data=clf_score_df, orient='h', color='black', size=8, alpha = 0.5)
plt.show()
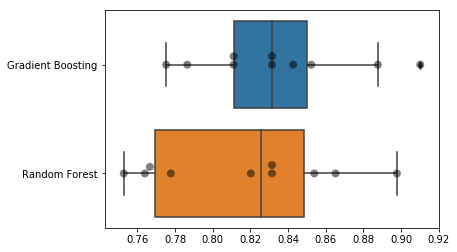
Gradient Boosting appears to have a slight edge over Random Forest, and it seems to perform more consistently, but performing a thorough grid search on the parameters of each will tell us for certain.
clf_features_df = pd.DataFrame.from_dict(clf_features_dict, orient='index')
clf_features_df.columns = X_train.columns.values
clf_features_df = pd.melt(clf_features_df.reset_index(),
id_vars = 'index',
var_name = 'feature',
value_name = 'importance').sort_values(by='importance').sort_values(by=['importance'])
sns.barplot(x='feature', y='importance', hue='index', palette='RdBu', data=clf_features_df)
plt.xticks(rotation=90)
plt.show()
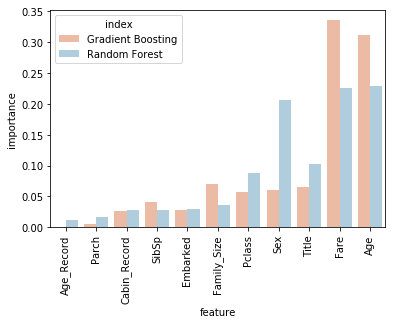
This reveals that we can drop "Age_Record", as neither algorithm is making much use of it. Everything on the graph to the left of "Pclass" could be a candidate from dropping to possibly improve accuracy, but first I will drop "Age_Record", "Cabin_Record", and "Embarked" tune each algorithm, and evaluate the results.
drop_list = ['Age_Record', 'Cabin_Record', 'Embarked']
X_train = X_train.drop(drop_list, axis=1)
x_test = x_test.drop(drop_list, axis=1)
xgb = XGBClassifier()
rfc = RandomForestClassifier()
clf_list = [xgb, rfc]
clf_name_list = ['Gradient Boosting', 'Random Forest']
xgb_params = {'max_depth': [5,7,9,12],
'learning_rate': [0.2, 0.1, 0.05, 0.01],
'n_estimators': [10, 25, 50, 100, 150, 200],
'min_child_weight': [1, 2, 3, 4, 5],
'gamma': [0, 1, 2, 3, 4, 5],
'random_state': [77]}
rfc_params = {'n_estimators': [250, 500, 750, 1000],
'max_features': [0.4, 0.6, 0.8, 1.0],
'max_depth': [15, 20, 25, 30],
'min_samples_leaf': [1, 2, 4, 8],
'random_state': [77]
}
cv_res = dict.fromkeys(clf_name_list)
clf_best = dict.fromkeys(clf_name_list)
for clf in clf_list:
clf_name = clf_name_list[clf_list.index(clf)]
if clf_name == 'Gradient Boosting':
param_grid = xgb_params
elif clf_name == 'Random Forest':
param_grid = rfc_params
clf_gs = GridSearchCV(clf, param_grid, cv=10, scoring='accuracy',
return_train_score=True)
clf_gs.fit(X_train, y_train)
clf_best[clf_name] = clf_gs.best_estimator_
cv_res[clf_name] = clf_gs.cv_results_
print('Best score: ', clf_gs.best_score_ * 100, '\n')
print('Using parameters: ', clf_gs.best_params_, '\n')
print('Fully described by: ', clf_gs.best_estimator_, '\n')
Best score: 84.3995510662
Using parameters: {'gamma': 1, 'learning_rate': 0.1, 'max_depth': 9, 'min_child_weight': 4, 'n_estimators': 25, 'random_state': 77}
Fully described by: XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bytree=1, gamma=1, learning_rate=0.1, max_delta_step=0,
max_depth=9, min_child_weight=4, missing=None, n_estimators=25,
n_jobs=1, nthread=None, objective='binary:logistic',
random_state=77, reg_alpha=0, reg_lambda=1, scale_pos_weight=1,
seed=None, silent=True, subsample=1)
Best score: 83.950617284
Using parameters: {'max_depth': 15, 'max_features': 0.8, 'min_samples_leaf': 4, 'n_estimators': 1000, 'random_state': 77}
Fully described by: RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=15, max_features=0.8, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=4, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=1000, n_jobs=1,
oob_score=False, random_state=77, verbose=0, warm_start=False)
I can now use the GridSearch results from from the above to investigate if any further fine tuning of parameters is likely to be beneficial for either classifier.
df_xgb_cvres = pd.DataFrame.from_dict(cv_res['Gradient Boosting'])
df_rfc_cvres = pd.DataFrame.from_dict(cv_res['Random Forest'])
fig = plt.figure(figsize=(16, 8))
ax1 = plt.subplot2grid((2,3),(0, 0))
ax2 = plt.subplot2grid((2,3),(0, 1))
ax3 = plt.subplot2grid((2,3),(1, 0))
ax4 = plt.subplot2grid((2,3),(1, 1))
ax5 = plt.subplot2grid((2,3),(1, 2))
ax2.yaxis.label.set_visible(False)
ax4.yaxis.label.set_visible(False)
ax5.yaxis.label.set_visible(False)
sns.boxplot(x=df_xgb_cvres['param_gamma'],
y=df_xgb_cvres['mean_test_score'], ax=ax1)
sns.boxplot(x=df_xgb_cvres['param_min_child_weight'],
y=df_xgb_cvres['mean_test_score'], ax=ax2)
sns.boxplot(x=df_xgb_cvres['param_learning_rate'],
y=df_xgb_cvres['mean_test_score'], ax=ax3)
sns.boxplot(x=df_xgb_cvres['param_max_depth'],
y=df_xgb_cvres['mean_test_score'], ax=ax4)
sns.boxplot(x=df_xgb_cvres['param_n_estimators'],
y=df_xgb_cvres['mean_test_score'], ax=ax5)
plt.show()
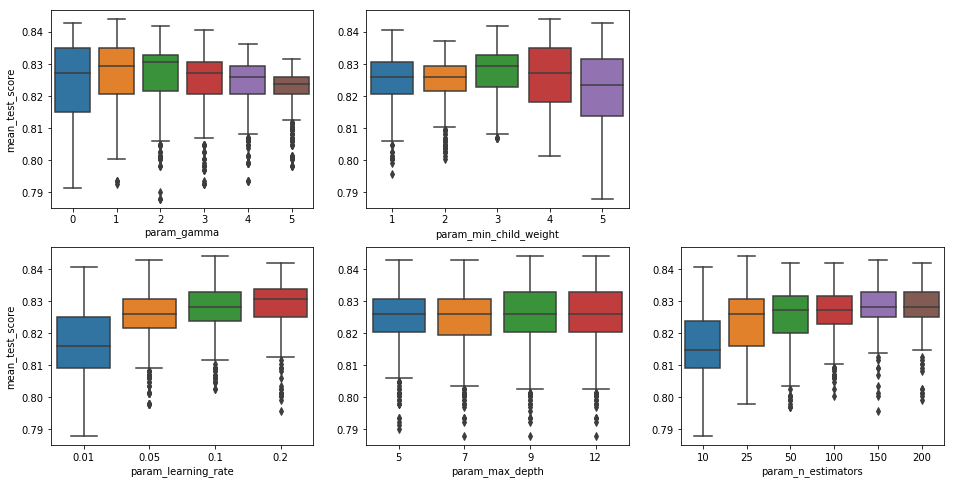
The best parameters returned by the CVGrid, for the random state assiged, were 'gamma': 1, 'learning_rate': 0.1, 'max_depth': 9, 'min_child_weight': 4, 'n_estimators': 25.
Each of the plots above appears to contain the peak value for each parameter, and it does not seems that much would be added by exploring additional parameters at either end of the range. However, it appears that the best parameters returned by CVGrid could benefit from some further tuning. I will explore this below.
fig = plt.figure(figsize=(12, 8))
ax1 = plt.subplot2grid((2,2),(0, 0))
ax2 = plt.subplot2grid((2,2),(0, 1))
ax3 = plt.subplot2grid((2,2),(1, 0))
ax4 = plt.subplot2grid((2,2),(1, 1))
ax2.yaxis.label.set_visible(False)
ax4.yaxis.label.set_visible(False)
sns.boxplot(x=df_rfc_cvres['param_min_samples_leaf'],
y=df_rfc_cvres['mean_test_score'], ax=ax1, palette = 'Accent_r')
sns.boxplot(x=df_rfc_cvres['param_max_features'],
y=df_rfc_cvres['mean_test_score'], ax=ax2, palette = 'Accent_r')
sns.boxplot(x=df_rfc_cvres['param_max_depth'],
y=df_rfc_cvres['mean_test_score'], ax=ax3, palette = 'Accent_r')
sns.boxplot(x=df_rfc_cvres['param_n_estimators'],
y=df_rfc_cvres['mean_test_score'], ax=ax4, palette = 'Accent_r')
plt.show()
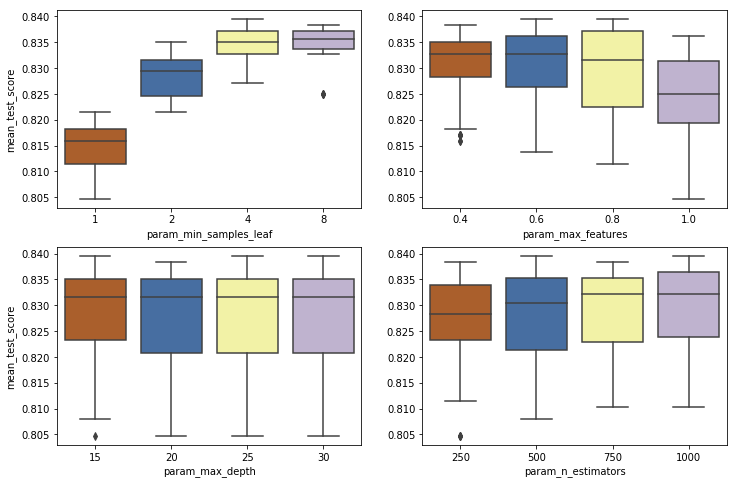
The best parameters returned by the CVGrid, for the random state assiged, were 'min_samples_leaf': 4, 'max_features': .8, 'max_depth': 15, 'n_estimators': 1000.
As with the gradient boosting classifier, each of the plots above appears to likely contain the peak value for each parameter, and it does not seems that much would be added by exploring additional parameters at either end of the range. There are a couple of parameters that appear as if they would benefit from further tuning. I will explore this below.
Further tuning to these algorithms yields a result that is in the top 5% of Kaggle.com submissions. Continue from here to discover which yields a better final score! Is it possibile to engineer additional features that might increase the score further?
